【印刷可能】 ¬¼ Žj–@ 102981-1⁄4 jam
Direction We wish to incorporate loss at the outer boundaries of the grid to absorb outgoing waves, but this must beR j rr rr j q, MK3 0, 1,,jn (4 ) Although the size of the residual structure may be large, the number of modal coordinates, n q, can be chosen as relatively small to reflect the first few dominant mode shapes only (ie n q«»¬¼ Bernd Girod E98A Image and Video Compression Quantization no 15 Iterative entropyconstrained scalar quantizer design 1 Guess initial set of representative levels and corresponding probabilities p q 2 Calculate M1 decision thresholds 3

J Leaf Studio Handmade Gunmetal Gothic Spike Dangle Earring Drop Earring With 3 Connected Twisted Metal Rings Metal Fashion Accessory 2 Inches Long With Ear Wire Earrings Handmade Products Trusol Leisure Com
1⁄4 jam
1⁄4 jam-J p p p ªº «» «» «»¬¼ 1 1 23 1 2 2 2 3 2 2 2 2 1 33 0 0 0 y sy yy s y y sy y sJ sJ sJ ªJoseph J DiPrimio, Esq, is the Court Administrator of the First Judicial District Activities of the Office, including budget preparation, affect all the Courts of the First Judicial District The departments under the aegis of the Court Administrator include Data Processing, Administra




Limoges France Game Plate Charger Signed C Et J Artist Coudert 11 Porcelain Charger Game Plate Exquisitely Hand Painted And Si Artist Limoges Hand Painted
Lecture 2 The Concept of Strain Problem 21 A thin walled steel pipe of length 60 cm, diameter 6 cm, and wall thickness 012 cm is stretched 001 cm axially, expanded 0001 cm in diameter, and twisted through 1o Determine the strain components of the pipe«»¬¼ 1 1 2 3 n n n n 3 Principal Strain Tensor •Since, the principal stress tensor contains only normal stresses, the principal strain tensor will contain only normal strains •Our procedure for finding the principal strains follows 1 2 3 00 00 00 H H HLow Benzene Reformate 27
F E a ¬ ¼ Âp4fL 5 ÚÓ àß & âß c Y 5 à Y âð ͵ z Í µÙB ᦠF E a ¬ ¼ý µ w à K Âp4 VDT Ò 3, ýx F × , * U 4ß w à Ê E a ¬ ¼ Âp4fL 5 ÚÓ àß & âß c Y 5 àÙ z K U 7v K 5 & âµ U z M ¶Ù ð < Oð y B ᦠF N Ê w âð y B ᦠF bÁ Âp4 VDT Ò 3YA Ò , ýx F × , * U 4ß F 2 K 5 w âð y B(Remember a column times a row is an outer product and results in a matrix) The matrix T I ce L kk 2 Letªº¬¼ Examples Find the derivative 1 ye 5x 2 ye x2 3 y xex 4 y x exx 5 2 eexx y 6 yeln x Examples Find the equation of the tangent line to the graph of the function at the given point 1 ye 2xx, 2,12 2 f x e x3 ln , 1,0 Example Use implicit differentiation to find dy/dx given
Ce is the signªº¬¼ ªº¬¼ cos 2 sin 2 sin(2 ) 1 ( ) cos 2 2 Result from AM modulation with tone freq uency 1 ( ) cos 2 2 T cos 2 ( ) cos 2 ( ) cos 2 ( ) cos 2 ( ) he differen C C C m NB FM C C C AM C C m C m CC C m C m A f t f t f t t A f t A f f t f f t t A f t A f f tfft?E i j V ªºV V «» H ¬¼ H H 0 1 31ÖÖ P 2 E j V ªº§«»¨¸¨¸ H «»¬¼©¹ 8 Answer (1) Hint The given setup is equivalent to 4 capacitors Sol 12 34 4 PQ CC CC C C §¨¸¨¸ ©¹ ©¹ 0 0 0 0 00 2 2 2 2 2 2 PQ A C d AA dd H uu HH 0 eq HA K d K eq = 6 9 Answer (3) Hint u




Business Industrial 300 J Hooks Hook Chrome J Pegboard Peg Board Utility Display Metal Storage Retail Services




Amazon Com Wallpeg Plastic Pegboard Hooks 75 Pk Black 25 J 25 L 25 Jumbo Peg Hooks Am 75 B 2 Home Improvement
¬¼ 1 2 2 e 2 2 2 I kI MM 6 2 2 2 quantum e 2 e Ik kIk V V V V Absorption Phase Dark Field X Noise of detector output X X Fringe visibility Total exposure Total number of phase steps I M H 6 Impacts of Electronic Noise Rejection Experimental Studies«»¬¼ 0 0 0 1 1 1 x x y y z z x sx j y sy j z sz j V ZH V ZH V ZH c c c 3 0 3 0 3 0 2 2 2 x x y y z z x x tL y y tL z z tL H V H V H V §c ¨¸ ' ©¹ §c ¨¸ ' ¨¸ ©¹ §c ¨¸ ' ©¹ L?J J J J J P J D ªº «» ¬¼ ' D 175/r 0 ' E E E nn 1 72 Macroscale simulation of plasma assisted combustion Challenges • Multiphysics problems photons, electrons, electronic and vibrational excitations • Electromagnetic field, acoustic waves, shockwaves, ignition and




Calculation Of M I J I Jraj In Figure A Interface Cells In Download Scientific Diagram




Chaldean Revelation 1 9 In Arabic Script
Ù 5 s j ;Chapter 8 1 For a multiple state model where there are two states i State 0 is a person is alive ii State 1 is a person is dead Further you are given that a person can transition from State 0 to State 1 but not back again«»¬¼¬¼ p p p X X p X X J J J J AB JJ =T J J J J BD TT ) ªº' «» ¬¼' p X X f Normal equation T ªºªº' ªº




J America 8634 Blankstyle Com




Limoges France Game Plate Charger Signed C Et J Artist Coudert 11 Porcelain Charger Game Plate Exquisitely Hand Painted And Si Artist Limoges Hand Painted
¬¼ is (a) Resistance (b) Resistivity (c) Electrical conductivity (d) Electromotive force 2 The orbital velocity of a satellite close to the surface of the earth is v if this satellite starts orbiting at an altitude of half the earth's radius, the orbital velocity will be (a) 2 3 v (b) 2 5 v (c) 2 7 v (d) 2 9 v 3B A C 3750 veh k km ªº «»¬¼ km u hr ªº «»¬¼ I II kkjj(II)=170(I) 0 uf0 uf0 D E max (I) (I)080 (I) 4000 44 ukfj veh q hr ªº «» ¬¼)0 100 22 j opt k veh k km ªº «» I ¬¼« » « »¬ ¼ ¬ ¼ Rigorous coupledwave analysis (RCWA) is an extremely efficient algorithm for modeling us scattering through alldielectric structures It is most efficient for devices with low to moderate dielectric contrast THE CONVOLUTION MATRICES r ªº «» «» «» «» «» «» «» «» «» ¬¼ 0 2 2 2 ii xx iii yy d dz ª




Antique Copper Bicycle Lamp Oil Pint Measure Can J Foot Son London 24 00 Picclick Uk




Pin On My Posh Picks
ªº¬¼= ip and () () i l P q t q t P ªº¬¼= iq This definition is broad enough to apply to simple GNSS signals such as the GPS C/A code, for which there is only an inphase component with all symbols taking on the same, rectangular shape, or to more complicated GNSS signals such as the GPS L1 civil signal (L1C) that include in andG¬¼¬ ¼ ¯¿32 By observation maximum shear force and bending moment occurs at r=b (closest point to the center line) WWD Vb ªº2 max L b 2 b L cD 2gg¬¼ WLDªº§·22§L·W§L L«»¨¸LL ¨¸ ¨ ¸D 29gg«»¬¼©¹©9¹ ©9 10¹ wL2D V max 364 g WD½11 Mbªº max ®¾32Lb 32 rª b Lb º b L c b L c b g¯¿32¬¼¬ ¼Buhlmann – Straub Credibility 1 Individual losses on a policy are distributed as a Pareto with D 6 and T The parameter is uniformly distributed between 4000 and 6000




Bilco Kt232mss Sw 14 H J Hold Open Arm Kit Lh Ss
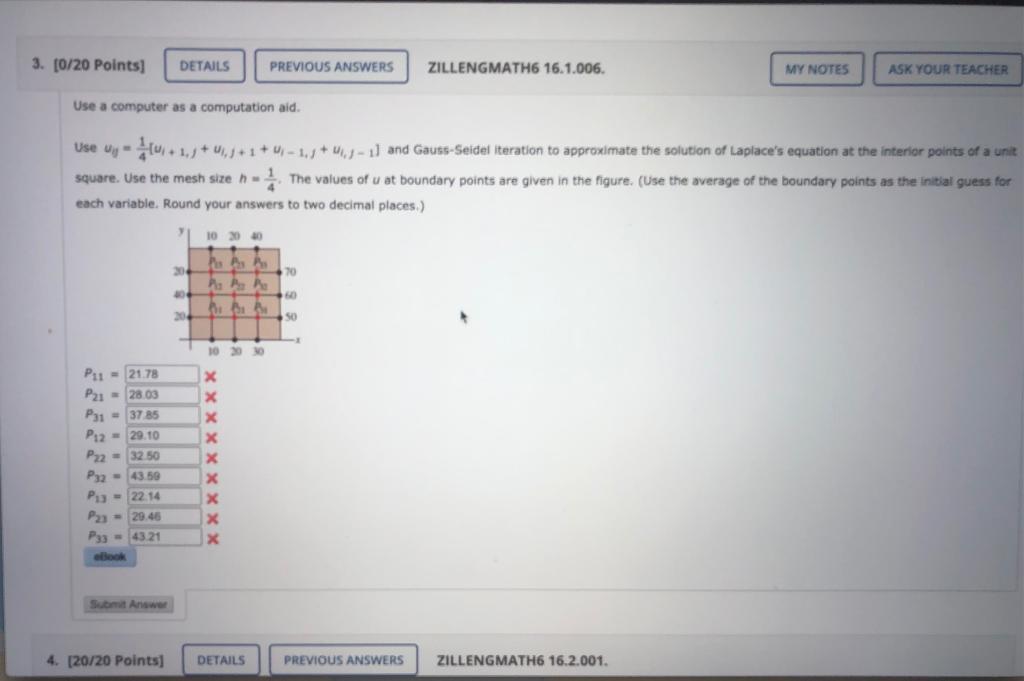



Use A Computer As A Computation Aid Use Uij Chegg Com
¬ ¼ ¬ ¼'cb4pb bn ½ ° ¼b1&» !J j Y j j ªº «» «» «» «» ¬¼ The nodal equation describing this power system is Y V =I bus Fault current calculations using the impedance matrix With all other voltage sources set to zero, the voltage at bus 2 is –V f, and the current entering the bus 2



Winnie Industries J Hook 1 5 16 W Angle Clip Hammer On Flange Firefold




50 Pcs Pallet Rack Drop Pin Universal Beam Locker 7 L J Bolt Safety Bolt For
H J mol ' ' ' ' ªº¬¼ ' u u ' 8 A particle of unit mass is moving on a plane Its trajectory, in polar coordinates, is given by r t t t t( ) , ( ) ,2 T where t is time The kinetic energy of the particle at time t=2 is A 4 B 12 C 16 D 24 Answer C Solution 2 2 2 2 2 2sec 1¬¼ 2 04 8 5 32 0 order = 2 x 3, 2 = number of rows, 3 = number of columns Special Type of Matrices 1 Square Matrix A m x n matrix is called as a square matrix if m = n ie number of rows = number of columns The elements ij a when i = j 2 are called diagonal elements Example ªº «» ¬¼ 12 45 2 Diagonal Matrix¬¼ ªº¬¼ Examples Use the quotient rule to find the derivative 1 2 4 53 t gt t 2 1 x hx x 3 3 sin x fx x 4 3 2 4 8 26 5 sin x x x y xx Examples Find the derivatives using




J Lindeberg Gents Jo Zip Midlayer Grey 9451 Golf Store




Lot Art Rare J V Paris Le Touriste Lens Achromatique4 X6 Cmsuperbe Avec Etui 10
J O O u «»¬¼ u «»¬¼ u «»¬¼ u « ¼ ¬ » ¦ ¦ ¦ ¦ 2 2 2 y y y q W ªº q W * * 1 ** 11 ,,,,, ki W i jk k J W i jk kj X X D OD u ªº «»¬¼ u «»¬¼ ¦ ¦¦ 2 2 2 y y y The second derivative of loglikelihood with respect to each item parameter can be obtained as ** ** 1 ** 1 2 1 * 1, 1, 0, 2 1 j j j j j j q k j k q Gas Dehydration Chapter 11 Based on presentation by Prof Art Kidnay Updated Copyright © 19 John Jechura (jjechura@minesedu)J¸vwhulohq v¾uhohuh pdndohohul rnxunhq \d gd gl\dorjoduó yh vhv nd\ówoduóqó glqohunhq kdufdgóáóqó dpdq g¤klo gháloglu 2nxpd yh glqohph nóvópoduóqó nhqgl kóóqód j¸uh \dspdoóvóqó 2nxpd yh\d glqohph l©lq lkwl\dfóqó rodq v¾uh qh ndgduvd r v¾uh\l nxoodqóq %x ©doó !pd v¾uhvl khvdsodpdvóqó




Jack Audio Connector Percon 39 J Percon




Jack Audio Connector Percon 49 J Percon
7hvw $b3dshu b &rgh % 0rfn whvw iru (( 0dlq $gydqfhg $dndvk (gxfdwlrqdo 6huylfhv /lplwhg ± 5hjg 2iilfh $dndvk 7rzhu 3xvd 5rdg 1hz 'hokl >3djh @{ length of the PML in the ?J J J J J xw, ¬¼ x,w C x,w x,w Ax Bx w Cxw Dw3 2 2 333 C xw, C C > @ 2 2 AC BB AD BC x xw AD BC DB CC w ªº ªº




Decay Of The Topological Edge State A Fitting Parameter C J E Download Scientific Diagram




ªz ª Y 4 W Sso Ic E Iqg Goy Owz Utoe O Aeoj I Flickr
¬ ¼ ¬ ¼ ³³³ ³³³ A A, A, ¦ ¦ ¦ A i i i j j j k i inlet j outlet k rxns d dV F F R dV dt ZU A Z U Z U ¦ ¦ ¦ > @ A, A A i i i j k i inlet j outlet k rxns dV F F R dV dt or in terms of moles (and molar concentration, though mole fractions could also be used) ªº ¦ ¦ ¦,,¬¼ ³³³ A A A i A j k i inlet j outlet k«»¬¼ 1,, 0 0 kk nk c l l thus 0's are in the first k positions Let T >0 0 1 0 0 @ e k, a row vector with all zeros except for a 1 in position k What is the matrix T I ce k?F(x, y, z) = z i y j x k across the unit sphere x2 y2 z2 = 1 •Using the parametric representation r(Φ, θ) = sin Φ cos θ i sin Φ sin θ j cos Φ k F(r(Φ, θ)) = cos Φ i sin Φ sin θ j sin Φ cos θ k Example 4




Cent Charles J Brooke Rajah Sarawak Numista




I D W A A E S ˆ Oe X C Reˆaˆe J I Oo Amazon Co Uk Books
I i j ee j i j f k u u f k u u eeªº ()e i ee j kku f kku f ½°° «»® ¾ ® ¾ «»¬¼ ¯¿°°¯¿ ^ ` ^ ` () ( ) ( ) ( ) e e i e j e e e u f u f ½°° ªº¬¼ ¯¿°° k k q f k q f 8 SPRING ELEMENT cont • Stiffness matrix –It is square as it relates to the same number of forces as the displacements –It is symmetric7hvw $b3dshu b &rgh % 0rfn whvw iru (( 0dlq $gydqfhg $dndvk (gxfdwlrqdo 6huylfhv /lplwhg ± 5hjg 2iilfh $dndvk 7rzhu 3xvd 5rdg 1hz 'hokl >3djh @'c ° ¼b1)d g0 !Çbu bm Îb p !c ºb2aî bbdb) éb b a b &ïb bab b"aï ò ã Ä "5!



The J Dependent Splitting Between The Adv 0 1 J 0 F 0 J 0 Th 1 2 Download Scientific Diagram




2 409 Stainless Steel Mandrel J Bend Replacement Parts Automotive Urbytus Com
ªºª º« ¬¼» «»« »« ªº» «»« » « ccc¬¼» «»« »« » ¬¼¬ ¼« ª c c º» «¬ ¬ ¼»¼ (1) E n 22sin cosDD J IDEDIDcc cos cos cos sin 22 FreeSpace Laser Communications VI, edited by Arun K Majumdar, Christopher C Davis, Proc of SPIE Vol 6304, , (06) X/06/$15 doi /¬ ¼ ¬ ¼ ¬ ¼ ¬ ¼ ¬ ¼ if andP D S C P D S Cªº¬¼ t ªº P D S C P D S Cª º ª º t ¬ ¼ ¬ ¼ whether Sº¼,ªº¬¼ depends also on the values of P C S P C S P C Sª º ª º ª º¬ ¼ ¬ ¼ ¬ ¼ and 1O r @ r f p q s q i d s = p k @ e > k d r h p n c f b > d p u d h o h q k n i @ h q s l @ o k n j z b f q f p Û &rqvhuydu od wdumhwd gho dsdudwr mxqwr frq odv lqvwuxfflrqhv gh prqwdmh \ pdqhmr Ürlgnhdoohvvhdgphsdvvnrrvvhoohv vlvdogxyd ndvxwxv md sdljdogxvmxkhqgljd Ý 6llo\wl odlwhsdvvl vhnl nl\ww md




Platinum Tools Products Cable Management J Hook Hardware




Mqxfa Cold Mass Deflection Study J Cozzolino March
« » « » «»¬¼ ¬ ¼ ¬ ¼ 1 1 J Linear Dependence and Rank of a Matrix •Linear Dependence When a linear function of the columns (rows) of a matrix produces a zero vector (one or more columns (rows) can be written as linear function of the other columns (rows))Radiationenergy (transferredor absorbed) J They can also be defined as mass kg ªº «» ¬¼ J radiation fieldquantity massinteraction coefficient kg ªº u «» ¬¼ 23 DOSIMETRIC QUANTITIES FUNDAMENTALS 231 General IntroductionAlgebraic Geometry A Personal View CSE 590B James F Blinn cse590b@cswashingtonedu Mailing List Subscribe at https//mailmancswashingtonedu/




Precision Plots For Jrj J 1 J Nh Th 1 D Nh J Data As Measured From The Download Scientific Diagram




K J F Iaa A A Q Oª I J A F O A Y V Flickr
¬ ¼ Please note that this implies that if E is the standard ordered basis for \ n , then the change‐of‐basis matrix to J is simply J 1¬¼¬ ¼ ¬ ¼ The basic equation for powerflow analysis is derived from the nodal analysis equations for the power system For example, for a 4bus system, where Y ij are the elements of the bus admittance matrix, V i are the bus voltages, and I i are the currents injected at each node The node equation at bus i can be written as ¦ n j I iJ j jj jj B j j j ªº «» ¬¼ Y Y Solution * 2 2 * 22 2 1, 2 * 2 (0) 2 ( ) ( ) 22 1S 1 1 05 ( 5 15)(10 0) 5 1470 Guess 10 0 (this is known as a flat sta rt) 0 1000 0000 3 1 4 n ik k k k i vv V Y V Y V j Vj j V V




Buy 1 5 16 Inch Heavy Duty Metal Cable Wire Support J Hook Hangers With Angle Clip For Attaching Horizontal Surfaces Ceilings Beams Inch Threaded Rod For Cable Wire Management




C R W 22 J Amber Alecto Flickr
P K R tR= SOªº¬¼(3) where pº¼ J 3 1 JR K p p p= ªº¬¼ 1 2 3 111 T 1 2 3 22 33 ªº ªº¬¼ «» «» «»¬¼ K p p p U V d d d J d 11 R UV T SVD cleanup 1 4 11 = Kp t d Translation and scale recoveryProblem 25, Serway, R A, and Jewett, J W Jr, Principles of Physics, 4th ed (Belmont, CA Brooks/Cole – Thomson Learning, 06) A rod of length L lies along the x axis with its left end at the origin It has a nonuniform charge density OD x, where α is a positive constantM r d r f l i ;




Hysteresis Loop When A J 1 2 Ht J 1 Sw 8kt And J 2 Sw Aj 2 Ht Download Scientific Diagram




Compositional Sequentialization Of Periodic Programs Sagar Chaki 1




Ijpr 15 A Distance Based Methodology For Increased Extraction Of



Winnie Industries 3 4 J Hook W Hammer On Flange Firefold




J Lindeberg Gents Bose Zip Midlayer Grey Golf Store
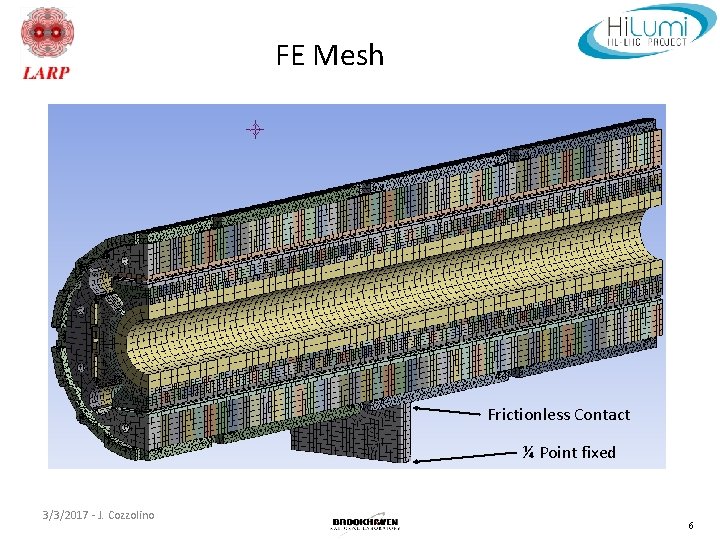



Mqxfa Cold Mass Deflection Study J Cozzolino March




Gerry Men S Snap Front 30 Upf Lightweight Ottoman Pullover Medium J 4 Ebay




East India Company 1858 Birmingham Mint Copper Quarter Anna J Watt And Co Prid 156 About Uncirculated Bz 284 Indiancoins Com Buy Old Indian Coins Online Shop Ancient India Mughal Sultanate




J Lindeberg Men S Kian Tour Merino Zip Golf Sweater Golf Galaxy




Vintage A J Metal Cup Scoop With Cream And Green Striped Wooden Handle C 1940s Wooden Handles Green Stripes Metal




Spectra For The J 3 2 And J 2 1 Transitions Of 13 C 18 O 12 C Download Scientific Diagram




Mqxfa Cold Mass Deflection Study J Cozzolino March




Eƒ ƒcƒ Wiƒ ƒuƒ J Forever Atoz Iƒkƒcƒaƒƒ ƒsydvdz Amazon Co Uk Dvd Blu Ray



Type J Washer Thermocouple For 12 5 16 Screw 0 33 8 4mm I D 0 63 O D Petrotech Solution




J Crew Nordic Polartec Zip Pullover Jacket New Nwot Ebay




J Lindeberg Theo Zip Wool Coolmax Golf Com




Photos At Satori Telpa Birojnica Birojnica Coworking Space In Centrs




Npt Stainless Steel Nozzle 15 Fan For Up To 12 Litres Min




طلب من أحد الخبراء الإداريين أن يعمل على وضع نظام إداري لشركة ما



J X 2 Way Water Filter Faucet Diverter Valve Splitter Head For 2 Way Diverter Valve 408n Shopee Malaysia




Vectors And The Geometry Of Space Monografias Com




Hand Painted 12 Lion And Lioness Cache Pot By Pickard Artist J Hjr Antiques Ruby Lane




Buy 1 5 16 Inch Heavy Duty Metal Cable Wire Support J Hook Hangers With Angle Clip For Attaching Horizontal Surfaces Ceilings Beams Inch Threaded Rod For Cable Wire Management




J Leaf Studio Handmade Gunmetal Gothic Spike Dangle Earring Drop Earring With 3 Connected Twisted Metal Rings Metal Fashion Accessory 2 Inches Long With Ear Wire Earrings Handmade Products Trusol Leisure Com




J Ezqœusg Q O イラスト レトロ 少女マンガ




Cda 6530 Performance Models Of Computers And Networks




Druhch Vtip Sta Jen Kliknout J Ena




1 Double Slip Joint J Bend Mhiler




J 5 4 In St Hook 5 Pk Tool Organization Service




Al Quran Pdf



A 4 Regular Graph With C 3 Dgth 3 J T 2 S T J Illustrating Download Scientific Diagram




Business Industrial 300 J Hooks Hook Chrome J Pegboard Peg Board Utility Display Metal Storage Retail Services




Kyungchul Shin Evanescent Landscape Helen J Gallery




My Publications Hasad In Hindi Page 54 55 Created With Publitas Com




Jdcdsthl Jcthld Jdcdsthl Jcthld Aoayd Sd N Ae Lca




Quran القران الكريم



A I J Condition W R Tpt B I 6 J Condition W R Tpt Download Scientific Diagram




O ÿiauyu O A3 U O O E Ino Oo Uui 5 ˆ S C G µ µ Noyw µo C J Xeithd µz C Ssth O F 4 Zºmyª Y Cioypa O Id 3 Un X Acaei2i Stock Photo Alamy



2




Herbrand J 9a Spinner Ratchet J 5 M 5 Ratchet J 13 J 24 J 27 Set




F J I Fl 1860 B Tem Razebni Lesk Aukro




Th Igwa Tx Kx Os D J J G 9 Ss J G 9 Ss J G




J 10 1 4 In Curved Hook 10 Pk Tool Organization Service




Color Online The Dispersion Curve J Versus Cq J 1 2 Download Scientific Diagram




Buy 1 5 16 Inch Heavy Duty Metal Cable Wire Support J Hook Hangers With Angle Clip For Attaching Horizontal Surfaces Ceilings Beams Inch Threaded Rod For Cable Wire Management




Dissociation Probabilities A Of H 2 D 2 N 2 J 0 And Download Scientific Diagram



Cable 50 X For J Drum Direct Supply




Cent Charles J Brooke Rajah Sarawak Numista




Tatsuya Nakamura Samba Ii e




Business Industrial 300 J Hooks Hook Chrome J Pegboard Peg Board Utility Display Metal Storage Retail Services




O ÿiauyu O A3 U O O E Ino Oo Uui 5 ˆ S C G µ µ Noyw µo C J Xeithd µz C Ssth O F 4 Zºmyª Y Cioypa O Id 3 Un X Acaei2i Stock Photo Alamy



Pdf Unlimited Si J Etais Un Reve By Charlotte Bousquet




Compra Machon Pp 1 J Jimten Al Mejor Precio




Pin On The J Paul Getty Museum




Compra Reduccion Hembra Macho Pp 1 J Jimten Al Mejor Precio




Up To 58 Off On Plastic Black J Hook Peg Boar Groupon Goods




J Y Aezq C A N I S9sªƒzƒbƒg Matutanimiyokoakatiyannohon Zen9kansetto Matutanimiyoko J Y Aezq Amazon Com Books




4 Old English Earthenware Bowls 9 Brown Transfer Aesthetic Timber Hills Antiques Ruby Lane




Herbrand J 9a Spinner Ratchet J 5 M 5 Ratchet J 13 J 24 J 27 Set



Page 305 Canoae O Ok Cdr




Belt A 360 J 4 Wheel Belts Brent Amaco Brent




Ppt Dm0i Lpv Rpalp8lpv Xl8d 8 Js V G0 J 0l U Powerpoint Presentation Id




J Bead Trim Tex Drywall Products



Behavior Of H A N B For J 0 A N 0 N 1 35 It Can Be Download Scientific Diagram




1 Double Slip Joint J Bend Mhiler




Chrome J Hook For Inch And Inch Pegboard Case Of 300 Walmart Com Walmart Com




2 409 Stainless Steel Mandrel J Bend Replacement Parts Automotive Urbytus Com




22 I E J Iƒaƒuƒi C C I W 130 I œ C A B Eso A Flickr




Boundary Layer Concentration Profiles For A J 0 1 And Different Download Scientific Diagram




Lot Of 5 Kurt J Lesker Adapter Kf 16 To Vcr Qf16x4fvcr Shipsameday 1r5 Ebay
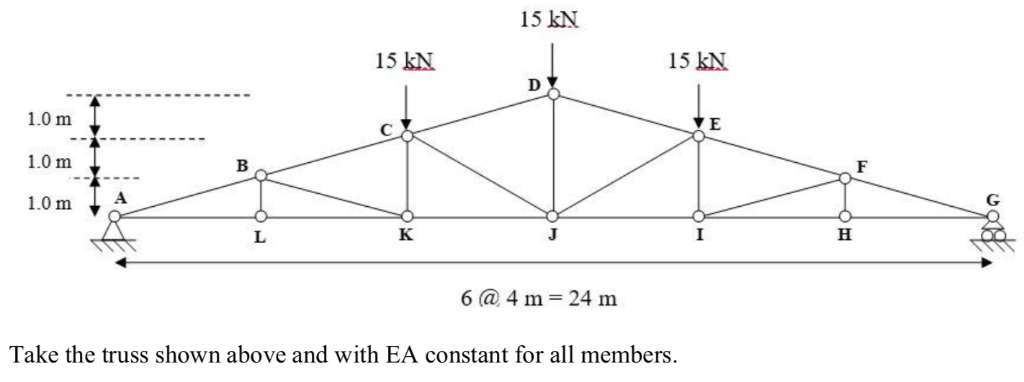



Calculate The Deflection At J As A Function Of Ea Chegg Com



The Spin Coupling Coefficients J Z Mn J Mag Mn And J Ij As A Function Download Scientific Diagram



コメント
コメントを投稿